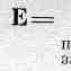En la práctica, a menudo se vuelve necesario encontrar la ley de distribución para la suma de variables aleatorias.

Que haya un sistema (XbX2) dos s continuas en. y su suma

Encontremos la densidad de distribución c. en. U. De acuerdo con la solución general del párrafo anterior, encontramos la región del plano donde x + x 2 (figura 9.4.1):

Derivando esta expresión con respecto a y, obtenemos una ap. variable aleatoria Y \u003d X + X 2:

Como la función φ (x b x 2) = Xj + x 2 es simétrica con respecto a sus argumentos, entonces

Si con. en. X y X 2 son independientes, entonces las fórmulas (9.4.2) y (9.4.3) toman la forma:

En el caso de que sea independiente c. en. x x y x2, hablar de la composición de las leyes de distribución. Producir composición dos leyes de distribución - esto significa encontrar la ley de distribución para la suma de dos independientes c. c., distribuidos de acuerdo con estas leyes. La notación simbólica se utiliza para designar la composición de las leyes de distribución.

que se denota esencialmente por las fórmulas (9.4.4) o (9.4.5).

Ejemplo 1. Se considera el trabajo de dos dispositivos técnicos (TD). Primero, TU funciona después de que su falla (falla) se incluye en la operación de TU 2. Tiempo de actividad TU TU TU 2 - x x y X 2 - son independientes y se distribuyen según leyes exponenciales con parámetros A,1 y X2 Por lo tanto, el tiempo Y funcionamiento sin problemas de la TU, que consta de TU! y TU 2 vendrá determinada por la fórmula

Se requiere encontrar un p.r. variable aleatoria Y, es decir, la composición de dos leyes exponenciales con parámetros y X2

Solución. Por la fórmula (9.4.4) obtenemos (y > 0)

Si existe una composición de dos leyes exponenciales con los mismos parámetros (?c = X 2 = Y), luego en la expresión (9.4.8) se obtiene una incertidumbre de tipo 0/0, ampliando la cual, se obtiene:

Comparando esta expresión con la expresión (6.4.8), estamos convencidos de que la composición de dos leyes exponenciales idénticas (?c = X 2 = X) es la ley de Erlang de segundo orden (9.4.9). Al componer dos leyes exponenciales con diferentes parámetros x x y A-2 obtener ley de Erlang generalizada de segundo orden (9.4.8). ?

Problema 1. La ley de distribución de la diferencia de dos s. en. Sistema con. en. (X y X 2) tiene un conjunto r.p./(x x x 2). Encuentra un p.r. sus diferencias Y=X - X2

Solución. Para el sistema con en. (Xb - X2) etc. será / (x b - x2), es decir, reemplazamos la diferencia con la suma. Por lo tanto, a.r. variable aleatoria U tendrá la forma (ver (9.4.2), (9.4.3)):

si un Con. en. X x iX 2 independiente, entonces

Ejemplo 2. Encuentra un f.r. la diferencia de dos s independientes distribuidas exponencialmente. en. con parámetros x x y X2

Solución. De acuerdo con la fórmula (9.4.11) obtenemos

Arroz. 9.4.2 Arroz. 9.4.3

La Figura 9.4.2 muestra una p. gramo(y). Si consideramos la diferencia de dos s independientes distribuidos exponencialmente. en. con la misma configuración (Ai= X 2 = PERO,), después gramo(y) \u003d / 2 - ya familiar

Ley de Laplace (Fig. 9.4.3). ?

Ejemplo 3. Encuentra la ley de distribución para la suma de dos independientes c. en. X y x2, distribuidos según la ley de Poisson con parámetros una x y un 2

Solución. Encuentre la probabilidad de un evento (X x + X 2 = t) (t = 0, 1,

Por lo tanto, S. en. Y = X x + X 2 distribuida según la ley de Poisson con el parámetro un x2) - un x + un 2. ?

Ejemplo 4. Encuentra la ley de distribución para la suma de dos independientes c. en. x x y x2, distribuidos según leyes binomiales con parámetros p x ri p 2 , pag respectivamente.

Solución. Imagina con. en. x x como:

dónde X1) - indicador de evento PERO wu "th experiencia:

Rango de distribución con. en. X,- tiene la forma

Haremos una representación similar para s. en. X2: donde X] 2) - indicador de evento PERO en y"-ésima experiencia:

Como consecuencia,

¿dónde está X? 1)+(2) si el indicador de evento PERO:

Así, hemos demostrado que en. Suegro cantidad (u + norte 2) indicadores de eventos PERO, de donde se sigue que el s. en. ^distribuido según la ley binomial con parámetros ( n x + n 2), pág.

Tenga en cuenta que si las probabilidades R en diferentes series de experimentos son diferentes, entonces como resultado de sumar dos s independientes. c., distribuidos según leyes binomiales, resulta c. c., distribuidos no según la ley del binomio. ?

Los ejemplos 3 y 4 se generalizan fácilmente a un número arbitrario de términos. Al componer las leyes de Poisson con parámetros a b a 2 , ..., a La ley de Poisson se obtiene nuevamente con el parámetro una (t) \u003d una x + una 2 + ... + y T.

Al componer leyes binomiales con parámetros (n r); (yo 2 , R) , (n t, p) nuevamente obtenemos la ley binomial con parámetros ("("), R), dónde norte (t) \u003d tu + norte 2 + ... + etc.

Hemos probado propiedades importantes de la ley de Poisson y la ley binomial: la "propiedad de estabilidad". La ley de distribución se llama sostenible, si la composición de dos leyes del mismo tipo da como resultado una ley del mismo tipo (solo difieren los parámetros de esta ley). En la Subsección 9.7 mostraremos que la ley normal tiene la misma propiedad de estabilidad.

Usemos el método general anterior para resolver un problema, a saber, encontrar la ley de distribución para la suma de dos variables aleatorias. Se tiene un sistema de dos variables aleatorias (X,Y) con densidad de distribución f(x,y). Considere la suma de las variables aleatorias X e Y: y encuentre la ley de distribución del valor Z. Para hacer esto, construimos una línea en el plano xOy, cuya ecuación es (Fig. 7). Esta es una línea recta que corta segmentos iguales a z en los ejes. La línea recta divide el plano xy en dos partes; a la derecha y encima de ella; izquierda y abajo.

La región D en este caso es la parte inferior izquierda del plano xOy, sombreada en la Fig. 7. Según la fórmula (16) tenemos:

Derivando esta expresión con respecto a la variable z incluida en el límite superior de la integral interior, obtenemos:

Esta es la fórmula general para la densidad de distribución de la suma de dos variables aleatorias.

Por razones de simetría del problema con respecto a X e Y, podemos escribir otra versión de la misma fórmula:

que es equivalente al primero y se puede usar en su lugar.

Un ejemplo de la composición de las leyes normales. Considere dos variables aleatorias independientes X e Y, sujetas a leyes normales:

Se requiere producir una composición de estas leyes, es decir, encontrar la ley de distribución de la cantidad: .

Aplicamos la fórmula general para la composición de las leyes de distribución:

Si abrimos los paréntesis en el exponente del integrando y traemos términos semejantes, obtenemos:

Sustituyendo estas expresiones en la fórmula que ya hemos encontrado

después de las transformaciones obtenemos:

y esto no es más que una ley normal con un centro de dispersión

y desviación estándar

Se puede llegar a la misma conclusión mucho más fácilmente con la ayuda del siguiente razonamiento cualitativo.

Sin abrir los paréntesis y sin realizar transformaciones en el integrando (17), inmediatamente llegamos a la conclusión de que el exponente es un trinomio cuadrado con respecto a x de la forma

donde el valor de z no está incluido en el coeficiente A en absoluto, el coeficiente B se incluye en primer grado y el coeficiente C se eleva al cuadrado. Teniendo esto en cuenta y aplicando la fórmula (18), concluimos que g(z) es una función exponencial cuyo exponente es un trinomio cuadrado con respecto a z, y la densidad de distribución; de este tipo corresponde a la ley normal. Así, nosotros; llegamos a una conclusión puramente cualitativa: la ley de distribución de z debe ser normal. Para encontrar los parámetros de esta ley - y - usamos el teorema de la suma de expectativas matemáticas y el teorema de la suma de varianzas. Por el teorema de la suma de las expectativas matemáticas. Por el teorema de la adición de la dispersión, o de donde se sigue la fórmula (20).

Pasando de desviaciones cuadráticas medias a desviaciones probables proporcionales a ellas, obtendremos: .

Así, hemos llegado a la regla siguiente: cuando se componen leyes normales, se obtiene de nuevo una ley normal, y se suman las expectativas y varianzas matemáticas (o desviaciones probables al cuadrado).

La regla de composición para leyes normales se puede generalizar al caso de un número arbitrario de variables aleatorias independientes.

Si hay n variables aleatorias independientes: sujetas a leyes normales con centros de dispersión y desviaciones estándar, entonces el valor también está sujeto a la ley normal con parámetros

En lugar de la fórmula (22), se puede utilizar una fórmula equivalente:

Si el sistema de variables aleatorias (X, Y) se distribuye de acuerdo con la ley normal, pero las cantidades X, Y son dependientes, entonces es fácil demostrar, como antes, con base en la fórmula general (6.3.1), que la ley de distribución de la cantidad es también una ley normal. Los centros de dispersión todavía se suman algebraicamente, pero para las desviaciones estándar la regla se vuelve más complicada: , donde r es el coeficiente de correlación de los valores de X e Y.

Al sumar varias variables aleatorias dependientes, que en su totalidad obedecen a la ley normal, la ley de distribución de la suma también resulta ser normal con parámetros

o probables desviaciones

donde es el coeficiente de correlación de las cantidades X i , X j , y la suma se extiende a todas las diferentes combinaciones de cantidades por pares.

Hemos visto una propiedad muy importante de la ley normal: cuando se combinan leyes normales, se obtiene nuevamente una ley normal. Esta es la llamada "propiedad de estabilidad". Se dice que una ley de distribución es estable si, al componer dos leyes de este tipo, se obtiene nuevamente una ley del mismo tipo. Hemos demostrado anteriormente que la ley normal es estable. Muy pocas leyes de distribución tienen la propiedad de estabilidad. La ley de densidad uniforme es inestable: al componer dos leyes de densidad uniforme en tramos de 0 a 1, obtenemos la ley de Simpson.

La estabilidad de una ley normal es una de las condiciones esenciales para su amplia aplicación en la práctica. Sin embargo, la propiedad de estabilidad, además de la normal, también la poseen algunas otras leyes de distribución. Una característica de la ley normal es que cuando se compone un número suficientemente grande de leyes de distribución prácticamente arbitrarias, la ley total resulta ser arbitrariamente cercana a la ley normal, independientemente de cuáles sean las leyes de distribución de los términos. Esto se puede ilustrar, por ejemplo, componiendo la composición de tres leyes de densidad uniforme en secciones de 0 a 1. La ley de distribución resultante g(z) se muestra en la fig. 8. Como se puede ver en el dibujo, la gráfica de la función g (z) es muy similar a la gráfica de la ley normal.

TEMA 3
	concepto de función de distribución
	expectativa matemática y varianza
	distribución uniforme (rectangular)
	distribución normal (gaussiana)
	Distribución
	t- Distribución del estudiante
	F- distribución
	distribución de la suma de dos variables aleatorias independientes
	ejemplo: distribución de la suma de dos independientes cantidades uniformemente distribuidas
	transformación de variables aleatorias
	ejemplo: distribución de una onda armónica con fase aleatoria
	teorema del límite central
	momentos de una variable aleatoria y sus propiedades
PROPÓSITO DEL CICLO CONFERENCIAS:		INFORME INFORMACIÓN INICIAL SOBRE LAS FUNCIONES DE DISTRIBUCIÓN MÁS IMPORTANTES Y SUS PROPIEDADES

FUNCIONES DE DISTRIBUCIÓN

Dejar x(k) es alguna variable aleatoria. Entonces para cualquier valor fijo x un evento aleatorio x(k) X definido como el conjunto de todos los resultados posibles k tal que x(k) x. En términos de la medida de probabilidad original dada en el espacio muestral, función de distribuciónP(x) definida como la probabilidad asignada a un conjunto de puntos k x(k) x. Tenga en cuenta que el conjunto de puntos k satisfaciendo la desigualdad x(k) x, es un subconjunto del conjunto de puntos que satisfacen la desigualdad x(k) . Formalmente

Es obvio que

Si el rango de valores de la variable aleatoria es continuo, como se supone a continuación, entonces densidad de probabilidad(unidimensional) p(x) está determinada por la relación diferencial

(4)

Como consecuencia,

(6)

Para poder considerar casos discretos es necesario admitir la presencia de funciones delta en la composición de la densidad de probabilidad.

VALOR ESPERADO

Sea la variable aleatoria x(k) toma valores del rango de -  a + . Significar(de lo contrario, valor esperado o valor esperado) x(k) se calcula utilizando el paso correspondiente al límite en la suma de productos de valores x(k) sobre la probabilidad de que estos eventos ocurran:

(8)

dónde mi- expectativa matemática de la expresión entre corchetes por índice k. La expectativa matemática de una función continua real de un solo valor se define de manera similar gramo(X) de una variable aleatoria x(k)

(9)

dónde p(x)- densidad de probabilidad de una variable aleatoria x(k). En particular, tomando g(x)=x, obtenemos cuadrado medio x(k) :

(10)

Dispersiónx(k) definido como el cuadrado medio de la diferencia x(k) y su valor medio,

es decir, en este caso g(x)= y

Por definición, Desviación Estándar variable aleatoria x(k), denotado , es el valor positivo de la raíz cuadrada de la varianza. La desviación estándar se mide en las mismas unidades que la media.

FUNCIONES DE DISTRIBUCIÓN MÁS IMPORTANTES

DISTRIBUCIÓN UNIFORME (RECTANGULAR).

Supongamos que el experimento consiste en una selección aleatoria de un punto del intervalo [ a, b] , incluidos sus puntos finales. En este ejemplo, como el valor de una variable aleatoria x(k) puede tomar el valor numérico del punto seleccionado. La función de distribución correspondiente tiene la forma

Por lo tanto, la densidad de probabilidad viene dada por la fórmula

En este ejemplo, el cálculo de la media y la varianza usando las fórmulas (9) y (11) da

DISTRIBUCIÓN NORMAL (GAUSSIANA)

, - media aritmética, - RMS.

El valor de z correspondiente a la probabilidad P(z)=1-, es decir

CHI - DISTRIBUCIÓN CUADRADA

Dejar - n variables aleatorias independientes, cada una de las cuales tiene una distribución normal con media cero y varianza unitaria.

Variable aleatoria chi-cuadrado con n grados de libertad.

densidad de probabilidad .

DF: 100 - puntos porcentuales - las distribuciones se denotan por , es decir,

la media y la varianza son iguales

t - DISTRIBUCIONES ESTUDIANTILES

y, z son variables aleatorias independientes; y - tiene - distribución, z - normalmente distribuida con media cero y varianza unitaria.

valor - tiene t- Distribución de Student con n grados de libertad

DF: 100 - punto porcentual t - se indica la distribución

La media y la varianza son iguales

F - DISTRIBUCIÓN

Variables aleatorias independientes; tiene - distribución con grados de libertad; distribución con grados de libertad. Valor aleatorio:

,

F es una variable aleatoria distribuida con y grados de libertad.

,

DF: 100 - punto porcentual:

La media y la varianza son iguales:

DISTRIBUCIÓN DE LA CANTIDAD

DOS VARIABLES ALEATORIAS

Dejar x(k) y y(k) son variables aleatorias que tienen una densidad de probabilidad conjunta p(x, y). Encuentre la densidad de probabilidad de la suma de variables aleatorias

en un fijo X tenemos y=z–x. Es por eso

en un fijo z valores X ejecute el intervalo de – a +. Es por eso

(37)

de donde se puede ver que para calcular la densidad deseada de la suma, se debe conocer la densidad de probabilidad conjunta original. si un x(k) y y(k) son variables aleatorias independientes que tienen densidades y, respectivamente, entonces y

(38)

EJEMPLO: LA SUMA DE DOS VARIABLES ALEATORIAS INDEPENDIENTES DISTRIBUIDAS UNIFORMEMENTE.

Sean dos variables aleatorias independientes con densidades de la forma

En otros casos Encontremos la densidad de probabilidad p(z) de su suma z= x+ y.

Densidad de probabilidad por es decir, para Como consecuencia, X menos que z. Además, no es igual a cero para Por la fórmula (38), encontramos que

Ilustración:

La densidad de probabilidad de la suma de dos variables aleatorias independientes distribuidas uniformemente.

CONVERSIÓN ALEATORIA

VALORES

Dejar x(t)- variable aleatoria con densidad de probabilidad p(x), Déjalo ir g(x) es una función continua real de un solo valor de X. Considere primero el caso cuando la función inversa x(g) es también una función continua de un solo valor de gramo. Densidad de probabilidad pag, correspondiente a una variable aleatoria g(x(k)) = g(k), se puede determinar a partir de la densidad de probabilidad p(x) variable aleatoria x(k) y derivado dg/dx bajo el supuesto de que la derivada existe y es diferente de cero, a saber:

(12)

Por lo tanto, en el límite dg/dx#0

(13)

Usando esta fórmula, sigue en su lado derecho en lugar de una variable X sustituir el valor apropiado gramo.

Considere ahora el caso cuando la función inversa x(g) es válida norte función valorada de gramo, dónde norte es un entero y todos los n valores son igualmente probables. Después

(14)

EJEMPLO:

DISTRIBUCIÓN DE LA FUNCIÓN ARMÓNICA.

Función armónica con amplitud fija X y frecuencia F será una variable aleatoria si su ángulo de fase inicial  =  (k)- valor aleatorio. En particular, deja t fijo e igual t o, y deje que la variable aleatoria armónica tenga la forma

pretendamos que  (k) tiene una densidad de probabilidad uniforme pags( ) tipo

Encuentre la densidad de probabilidad p(x) variable aleatoria x(k).

En este ejemplo, la función directa X( ) inequívocamente, y la función inversa  (X) ambiguo.

Definición. Las variables aleatorias Х 1 , Х 2 , …, Х n se llaman independientes si para cualquier x 1, x 2 , …, x n los eventos son independientes

(ω: X 1 (ω)< x},{ω: Х 2 (ω) < x},…, {ω: Х n (ω) < x n }.

De la definición se sigue directamente que para variables aleatorias independientes X 1, 2x2, …, X norte función de distribución norte-variable aleatoria dimensional X = X 1, 2x2, …, X norte es igual al producto de funciones de distribución de variables aleatorias X 1, 2x2, …, X norte

F(x1 , x2, …, x norte) = F(x1)F(x2)…F(x norte). (1)

Derivamos la igualdad (1) norte veces por x1 , x2, …, x norte, obtenemos

pags(x1 , x2, …, x norte) = pags(x1)pags(x2)…pags(x norte). (2)

Se puede dar otra definición de la independencia de las variables aleatorias.

Si la ley de distribución de una variable aleatoria no depende de los posibles valores que hayan tomado otras variables aleatorias, entonces tales variables aleatorias se denominan independientes en conjunto.

Por ejemplo, se compran dos billetes de lotería de diferentes ediciones. Dejar X– la cantidad de ganancias por el primer boleto, Y– la cantidad de ganancias para el segundo boleto. variables aleatorias X y Y- independiente, ya que la adjudicación de un boleto no afectará la ley de distribución del otro. Pero si los boletos son del mismo tema, entonces X y Y- dependiente.

Dos variables aleatorias se denominan independientes si la ley de distribución de una de ellas no cambia según los posibles valores que haya tomado la otra variable.

Teorema 1(circunvoluciones) o "el teorema de la densidad de la suma de 2 variables aleatorias".

Dejar X = (X 1;2x2) es una variable aleatoria bidimensional continua independiente, Y = X 1+ 2x2. Entonces la densidad de distribución

Prueba. Se puede demostrar que si , entonces

dónde X = (X 1 , X 2 , …, X norte). Entonces sí X = (X 1 , X 2), entonces la función de distribución Y = X 1 + X 2 se puede definir de la siguiente manera (Fig. 1) -

De acuerdo con la definición, la función es la densidad de distribución de la variable aleatoria Y = X 1 + X 2 , es decir

pía (t) = que se iba a demostrar.

Derivamos una fórmula para encontrar la distribución de probabilidad de la suma de dos variables aleatorias discretas independientes.

Teorema 2. Dejar X 1 , X 2 – variables aleatorias discretas independientes,

Prueba. Imagina un evento una x = {X 1 +X 2 = X) como una suma de eventos incompatibles

una x = å( X 1 = X i ; X 2 = X– X i).

Porque X 1 , X 2 - independiente entonces PAGS(X 1 = X i ; X 2 = X– X yo) = PAGS(X 1 = X i) PAGS(X 2 = xx entonces yo

PAGS(una x) = PAGS(å( X 1 = X i ; X 2 = x – x yo)) = å( PAGS(X 1 = x yo) PAGS(X 2 = xx i))

QED

Ejemplo 1 Dejar X 1 , X 2 - variables aleatorias independientes que tienen una distribución normal con parámetros norte(0;1); X 1 , X 2 ~ norte(0;1).

Encontremos la densidad de distribución de su suma (denotamos X 1 = X, Y = X 1 +X 2)

Es fácil ver que el integrando es la densidad de distribución de una variable aleatoria normal con parámetros a= , , es decir la integral es 1

Función pía(t) es la densidad de la distribución normal con parámetros a = 0, s = . Así, la suma de variables aleatorias normales independientes con parámetros (0,1) tiene una distribución normal con parámetros (0,), es decir Y = X 1 + X 2 ~ norte(0;).

Ejemplo 2. Sean dadas dos variables aleatorias independientes discretas con distribución de Poisson, entonces

dónde k, m, n = 0, 1, 2, …,¥.

Por el Teorema 2 tenemos:

Ejemplo 3 Dejar X 1, X 2- Variables aleatorias independientes con distribución exponencial. Encontremos la densidad Y= X 1 +X 2 .

Denotar X = X 1. Desde X 1, X 2 son variables aleatorias independientes, entonces usamos el "teorema de convolución"

Se puede demostrar que si la suma ( yo tienen una distribución exponencial con parámetro l), entonces Y= tiene una distribución llamada distribución de Erlang ( norte- 1) orden. Esta ley se obtuvo modelando el funcionamiento de las centrales telefónicas en los primeros trabajos sobre la teoría de las colas.

En estadística matemática, las leyes de distribución se utilizan a menudo para variables aleatorias que son funciones de variables aleatorias normales independientes. Consideremos tres leyes que se encuentran con mayor frecuencia en el modelado de fenómenos aleatorios.

Teorema 3. Si las variables aleatorias son independientes X 1, ..., X norte, entonces las funciones de estas variables aleatorias también son independientes Y 1 = F 1 (X 1), ...,S n = fn(X norte).

Distribución Pearson(desde 2 -distribución). Dejar X 1, ..., X norte son variables aleatorias normales independientes con parámetros a= 0, s = 1. Componga una variable aleatoria

De este modo,

Se puede demostrar que la densidad para x > 0 tiene la forma , donde k n es algún coeficiente para que se cumpla la condición. Como n ® ¥, la distribución de Pearson tiende a la distribución normal.

Sea Х 1 , Х 2 , …, Хn ~ N(a,s), luego las variables aleatorias ~ N(0,1). Por tanto, la variable aleatoria tiene una distribución c 2 con n grados de libertad.

La distribución de Pearson se tabula y se usa en diversas aplicaciones de las estadísticas matemáticas (por ejemplo, al probar la hipótesis de que la ley de distribución es consistente).

El tomador de decisiones puede usar seguros para mitigar el impacto financiero adverso de ciertos tipos de eventos aleatorios.

Pero esta consideración es muy general, ya que un tomador de decisiones podría significar tanto un individuo que busca protección contra daños a la propiedad, ahorros o ingresos, como una organización que busca protección contra el mismo tipo de daño.

De hecho, tal organización puede ser una compañía de seguros que está buscando formas de protegerse de pérdidas financieras debido a demasiados eventos asegurados que han ocurrido con un cliente individual o con su cartera de seguros. Esta protección se llama reaseguro.

Considere uno de dos modelos (es decir, modelo de riesgo individual) ampliamente utilizado en la determinación de tasas y reservas de seguros, así como en reaseguros.

Denotamos por S el monto de las pérdidas accidentales de la compañía de seguros por alguna parte de sus riesgos. En este caso S es una variable aleatoria para la que tenemos que determinar la distribución de probabilidad. Históricamente, para distribuciones de r.v. S había dos conjuntos de postulados. El modelo de riesgo individual define S de la siguiente manera:

donde rv significa las pérdidas causadas por el objeto del seguro con el número i, a norte denota el número total de objetos de seguro.

Se suele suponer que son variables aleatorias independientes, ya que en este caso los cálculos matemáticos son más sencillos y no se requiere información sobre la naturaleza de la relación entre ellas. El segundo modelo es el modelo de riesgo colectivo.

El modelo considerado de riesgos individuales no refleja cambios en el valor del dinero a lo largo del tiempo. Esto se hace para simplificar el modelo, por lo que el título del artículo se refiere a un intervalo de tiempo corto.

Consideraremos solo modelos cerrados, es decir. aquellos en los que el número de objetos de seguro norte en la fórmula (1.1) se conoce y se fija al comienzo del intervalo de tiempo considerado. Si introducimos supuestos sobre la presencia de migración desde o hacia el sistema de seguros, obtenemos un modelo abierto.

Variables aleatorias que describen pagos individuales

En primer lugar, recordemos las principales disposiciones relativas a los seguros de vida.

En caso de seguro de muerte por un período de un año, el asegurador se obliga a pagar la cantidad b, si el tomador fallece dentro del año siguiente a la fecha de celebración del contrato de seguro, y no paga nada si el tomador vive este año.

La probabilidad de que ocurra un evento asegurado durante el año especificado se denota por .

La variable aleatoria que describe los pagos de seguros tiene una distribución que puede especificarse mediante la función de probabilidad

(2.1)

o la función de distribución correspondiente

(2.2)

De la fórmula (2.1) y de la definición de momentos, obtenemos

(2.4)

Estas fórmulas también se pueden obtener escribiendo X como

donde es un valor constante pagado en caso de muerte, y es una variable aleatoria que toma el valor 1 en caso de muerte y 0 en caso contrario.

Así, y , y el valor medio y la varianza de la v.r. son iguales y respectivamente, y el valor medio y la varianza de r.v. son iguales a y , lo que coincide con las fórmulas anteriores.

Una variable aleatoria con rango (0,1) es ampliamente utilizada en modelos actuariales.

En los libros de texto sobre la teoría de la probabilidad, se llama indicador, Bernoulli al azar valor o variable aleatoria binomial en el diseño de prueba única.

la llamaremos indicador por razones de brevedad, y también porque indica el inicio, o no inicio, del evento en cuestión.

Volvamos a la búsqueda de modelos más generales en los que el valor del pago del seguro también sea una variable aleatoria y varios eventos de seguro puedan ocurrir en el intervalo de tiempo considerado.

El seguro de salud, el seguro de automóviles y otros seguros de propiedad y el seguro de responsabilidad civil brindan inmediatamente muchos ejemplos. Generalizando la fórmula (2.5), establecemos

donde es una variable aleatoria que describe los pagos de seguros en el intervalo de tiempo considerado, r.v. denota la cantidad total de pagos en este intervalo y r.v. es un indicador del evento de que al menos un evento asegurado ha ocurrido.

Siendo un indicador de tal evento, r.v. corrige la presencia () o falta () eventos asegurados en este intervalo de tiempo, pero no el número de eventos asegurados en él.

La probabilidad seguirá siendo denotada por .

Analicemos varios ejemplos y determinemos la distribución de variables aleatorias y en algún modelo.

Consideremos primero un seguro de muerte por un año, con un beneficio adicional si la muerte es un accidente.

Para mayor precisión, supongamos que si la muerte se produjo como resultado de un accidente, entonces el monto del pago será de 50 000. Si la muerte se produce por otras causas, el monto del pago será de 25 000.

Supongamos que para una persona de una determinada edad, estado de salud y profesión, la probabilidad de morir a consecuencia de un accidente durante el año es 0,0005, y la probabilidad de morir por otras causas es 0,0020. En forma de fórmula, se ve así:

Sumando todos los valores posibles de , obtenemos

,

Distribución condicional c. en. condición tiene la forma

Considere ahora el seguro de colisión de automóviles (compensación pagada al propietario del automóvil por los daños causados ​​a su automóvil) con un deducible incondicional de 250 y un pago máximo de 2000.

Para mayor claridad, asumimos que la probabilidad de ocurrencia de un evento asegurado en el período de tiempo considerado para un individuo es 0.15, y la probabilidad de ocurrencia de más de una colisión es igual a cero:

, .

La suposición poco realista de que no puede ocurrir más de un evento asegurado durante un período se hace para simplificar la distribución de r.v. .

Dejaremos de lado esta suposición en la siguiente sección después de considerar la distribución de la suma de varios reclamos de seguros.

Dado que es el valor de los pagos del asegurador, y no los daños causados ​​al automóvil, podemos considerar dos características, y.

En primer lugar, el evento incluye aquellas colisiones en las que el daño es menor que el deducible incondicional, que es de 250.

En segundo lugar, la distribución de r.v. tendrá un "coágulo" de la masa probabilística en el punto del monto máximo de los pagos del seguro, que es igual a 2000.

Suponga que la masa probabilística concentrada en este punto es 0,1. Además, suponga que el valor de los pagos de seguros en el intervalo de 0 a 2000 puede modelarse mediante una distribución continua con una función de densidad proporcional a (En la práctica, la curva continua que se elige para representar la distribución de primas es el resultado de estudios de primas en el período anterior).

Resumiendo estos supuestos sobre la distribución condicional de r.v. bajo la condición , llegamos a una distribución de tipo mixto que tiene una densidad positiva en el rango de 0 a 2000 y algún "coágulo" de la masa probabilística en el punto 2000. Esto se ilustra en el gráfico de la Fig. 2.2.1.

La función de distribución de esta distribución condicional se ve así:

Figura 2.1. Función de distribución de r.v. B bajo la condición I = 1

Calculamos la expectativa matemática y la varianza en el ejemplo considerado con seguro de automóvil de dos maneras.

Primero, escribimos la distribución de la r.v. y utilícelo para calcular y . Denotando a través de la función de distribución de la r.v. , tenemos

Para X<0

Esta es una distribución mixta. Como se muestra en la fig. 2.2, tiene una parte discreta ("grupo" de masa probabilística en el punto 2000) y una parte continua. Tal función de distribución corresponde a una combinación de la función de probabilidad

Arroz. 2.2. Función de distribución de r.v. X=IB

y funciones de densidad

En particular, y . Es por eso .

Hay una serie de fórmulas que relacionan los momentos de variables aleatorias con expectativas matemáticas condicionales. Para la expectativa matemática y para la varianza, estas fórmulas tienen la forma

(2.10)

(2.11)

Se supone que las expresiones del lado izquierdo de estas igualdades se calculan directamente a partir de la distribución de la r.v. . Al calcular las expresiones de los lados derechos, a saber, y , se usa la distribución condicional de la r.v. a un valor fijo de r.v. .

Estas expresiones son, por tanto, funciones de la r.v. , y podemos calcular sus momentos usando la distribución de r.v. .

Las distribuciones condicionales se utilizan en muchos modelos actuariales y esto permite que las fórmulas anteriores se apliquen directamente. En nuestro modelo. Teniendo en cuenta la r.v. como y rv como, obtenemos

(2.12)

, (2.14)

, (2.15)

y considerar expectativas matemáticas condicionales

(2.16)

(2.17)

Las fórmulas (2.16) y (2.17) se definen en función de la v.r. , que se puede escribir como la siguiente fórmula:

Desde entonces (2.21)

Porque tenemos y (2.22)

Las fórmulas (2.21) y (2.22) se pueden combinar: (2.23)

Así, (2.24)

Sustituyendo (2.21), (2.20) y (2.24) en (2.12) y (2.13), obtenemos

Aplicaremos las fórmulas recibidas para el cálculo y en el ejemplo del seguro de automóvil (fig. 2.2). Dado que la función de densidad de la r.v. En la condición se expresa por la fórmula

y P(B=2000|I=1)= 0.1, tenemos

Finalmente, suponiendo q= 0.15, de las fórmulas (2.25) y (2.26) obtenemos las siguientes igualdades:

Para describir otra situación de seguro, podemos ofrecer otros modelos para r.v. .

Ejemplo: modelo para el número de muertes por accidentes de aviación

Como ejemplo, considere un modelo para el número de muertes debido a accidentes de aviación durante un período de un año de operación de una aerolínea.

Podemos comenzar con una variable aleatoria que describa el número de muertes para un vuelo y luego sumar estas variables aleatorias sobre todos los vuelos en un año.

Para un vuelo, el evento indicará el inicio de un accidente aéreo. El número de muertos que supuso esta catástrofe estará representado por el producto de dos variables aleatorias y , donde es el factor de ocupación de la aeronave, es decir, el número de personas a bordo en el momento del accidente, y es la proporción de muertos entre las personas a bordo. junta.

El número de muertes se presenta de esta manera, ya que las estadísticas separadas para y son más accesibles que las estadísticas para r.v. . Entonces, aunque la proporción de muertes entre las personas a bordo y el número de personas a bordo probablemente estén relacionadas, como primera aproximación se puede suponer que la r.v. e independiente

Sumas de variables aleatorias independientes

En el modelo de riesgo individual, los pagos de seguros realizados por una compañía de seguros se presentan como la suma de los pagos a muchos individuos.

Recuerde dos métodos para determinar la distribución de la suma de variables aleatorias independientes. Considere primero la suma de dos variables aleatorias, cuyo espacio muestral se muestra en la Fig. 3.1.

Arroz. 2.3.1. Evento

La línea y el área debajo de esta línea representan un evento. Por lo tanto, la función de distribución de la r.v. S tiene la forma (3.1)

Para dos variables aleatorias discretas no negativas, podemos usar la fórmula de probabilidad total y escribir (3.1) como

si un X y Y son independientes, la última suma se puede reescribir como

(3.3)

La función de probabilidad correspondiente a esta función de distribución se puede encontrar mediante la fórmula

(3.4)

Para variables aleatorias continuas no negativas, las fórmulas correspondientes a las fórmulas (3.2), (3.3) y (3.4) tienen la forma

Cuando una o ambas variables aleatorias X y Y tienen una distribución de tipo mixta (que es típica de los modelos de riesgo individual), las fórmulas son similares, pero más engorrosas. Para variables aleatorias que también pueden tomar valores negativos, las sumas e integrales de las fórmulas anteriores se toman sobre todos los valores de y desde hasta .

En la teoría de la probabilidad, la operación de las fórmulas (3.3) y (3.6) se denomina convolución de dos funciones de distribución y se denota por . La operación de convolución también se puede definir para un par de funciones de probabilidad o densidad utilizando las fórmulas (3.4) y (3.7).

Para determinar la distribución de la suma de más de dos variables aleatorias, podemos usar iteraciones del proceso de convolución. Para , donde son variables aleatorias independientes, denota la función de distribución de la r.v., y es la función de distribución de la r.v. , Nosotros recibiremos

El ejemplo 3.1 ilustra este procedimiento para tres variables aleatorias discretas.

Ejemplo 3.1. Las variables aleatorias son independientes y tienen distribuciones definidas por las columnas (1), (2) y (3) de la siguiente tabla.

Escribamos la función de probabilidad y la función de distribución de la r.v.

Solución. La tabla usa la notación presentada antes del ejemplo:

Las columnas (1)-(3) contienen la información disponible.

La columna (4) se obtiene de las columnas (1) y (2) usando (3.4).

La columna (5) se obtiene de las columnas (3) y (4) utilizando (3.4).

La definición de la columna (5) completa la determinación de la función de probabilidad para la r.v. . Su función de distribución en la columna (8) es el conjunto de sumas parciales de la columna (5), comenzando desde arriba.

Para mayor claridad, hemos incluido la columna (6), la función de distribución para la columna (1), la columna (7), que se puede obtener directamente de las columnas (1) y (6) usando (2.3.3), y la columna (8 ) determinado por de manera similar para las columnas (3) y (7). La columna (5) se puede determinar a partir de la columna (8) por sustracción sucesiva.

Volvamos a la consideración de dos ejemplos con variables aleatorias continuas.

Ejemplo 3.2. Deja que r.v. tiene una distribución uniforme en el intervalo (0,2), y sea la v.r. no depende de la r.v. y tiene una distribución uniforme en el intervalo (0,3). Definamos la función de distribución de la r.v.

Solución. Dado que las distribuciones de r.v. y continua, usamos la fórmula (3.6):

Después

Espacio muestral de r.v. y se ilustra en la Fig. 3.2. El área rectangular contiene todos los valores posibles del par y . El evento que nos interesa, , se representa en la figura para cinco valores s.

Para cada valor, la línea interseca el eje. Y en el punto s y una línea en un punto. Los valores de la función para estos cinco casos se describen mediante la siguiente fórmula:

Arroz. 3.2. Convolución de dos distribuciones uniformes

Ejemplo 3.3. Consideremos tres v.r. independientes. . para rv tiene una distribución exponencial y . Encontremos la función de densidad de la r.v. aplicando la operación de convolución.

Solución. Tenemos

Usando la fórmula (3.7) tres veces, obtenemos

Otro método para determinar la distribución de la suma de variables aleatorias independientes se basa en la unicidad de la función generadora de momentos, que para r.v. está determinada por la relación .

Si esta expectativa matemática es finita para todos t de algún intervalo abierto que contenga el origen, entonces es la única función generadora de los momentos de distribución de la v.r. en el sentido de que no existe otra función que no sea , que sería la función generadora de los momentos de distribución de la r.v. .

Esta unicidad se puede utilizar de la siguiente manera: para la suma

Si son independientes, entonces la expectativa del producto en la fórmula (3.8) es igual a ..., asi que

Encontrar una expresión explícita para la única distribución que corresponde a la función generadora de los momentos (3.9) completaría el hallazgo de la distribución de la r.v. . Si no es posible especificarlo explícitamente, entonces se puede buscar por métodos numéricos.

Ejemplo 3.4. Considere las variables aleatorias del ejemplo 3.3. Definamos la función de densidad de la r.v. , utilizando la función generadora de los momentos de la r.v. .

Solución. De acuerdo con la igualdad (3.9), que se puede escribir como utilizando el método de descomposición en fracciones simples. La solucion es . Pero es la función generadora de los momentos de la distribución exponencial con el parámetro , por lo que la función de densidad de la r.v. tiene la forma

Ejemplo 3.5. En el estudio de procesos aleatorios se introdujo la distribución gaussiana inversa. Se utiliza como distribución de r.v. A, el monto de los pagos del seguro. La función de densidad y la función generatriz de los momentos de la distribución gaussiana inversa están dadas por las fórmulas

Encontremos la distribución de r.v. , donde r.v. son independientes y tienen las mismas distribuciones gaussianas inversas.

Solución. Usando la fórmula (3.9), obtenemos la siguiente expresión para la función generadora de los momentos r.v. :

La función generadora de los momentos corresponde a una distribución única, y se puede observar que tiene una distribución gaussiana inversa con parámetros y .

Aproximaciones para la distribución de la suma

El teorema del límite central proporciona un método para encontrar valores numéricos para la distribución de la suma de variables aleatorias independientes. Por lo general, este teorema se formula para la suma de variables aleatorias independientes e idénticamente distribuidas, donde .

Para cualquier n, la distribución de la r.v. donde = , tiene esperanza matemática 0 y varianza 1. Como se sabe, la secuencia de tales distribuciones (por norte= 1, 2, ...) tiende a la distribución normal estándar. Cuando norte grande, este teorema se aplica para aproximar la distribución de r.v. distribución normal con media μ y dispersión. Del mismo modo, la distribución de la suma norte variables aleatorias se aproxima mediante una distribución normal con media y varianza.

La eficiencia de tal aproximación depende no solo del número de términos, sino también de la proximidad de la distribución de términos a la normal. Muchos cursos elementales de estadística establecen que n debe ser al menos 30 para que la aproximación sea razonable.

Sin embargo, uno de los programas para generar variables aleatorias normalmente distribuidas que se usa en el modelado de simulación implementa una variable aleatoria normal como un promedio de 12 variables aleatorias independientes distribuidas uniformemente en el intervalo (0,1).

En muchos modelos de riesgo individual, las variables aleatorias incluidas en las sumas no se distribuyen por igual. Esto se ilustrará con ejemplos en la siguiente sección.

El teorema del límite central también se extiende a secuencias de variables aleatorias desigualmente distribuidas.

Para ilustrar algunas aplicaciones del modelo de riesgo individual, utilizaremos una aproximación normal de la distribución de la suma de variables aleatorias independientes para obtener soluciones numéricas. si un , después

y además, si r.v. independiente, entonces

Para la aplicación en cuestión, solo necesitamos:

• encontrar los promedios y varianzas de variables aleatorias que simulan pérdidas individuales,
• sumarlos para obtener el promedio y la varianza de las pérdidas de la compañía de seguros en su conjunto,
• utilice la aproximación normal.

A continuación ilustramos esta secuencia de acciones.

Solicitudes de seguro

Esta sección ilustra el uso de la aproximación normal con cuatro ejemplos.

Ejemplo 5.1. Una compañía de seguros de vida ofrece un contrato de seguro de muerte de un año con pagos de 1 y 2 unidades a personas cuyas probabilidades de muerte son 0.02 o 0.01. La siguiente tabla muestra el número de personas nk en cada una de las cuatro clases formadas de acuerdo con el pago b k y la probabilidad de un evento asegurado qq:

k	q k	b k	nk
1	0,02	1	500
2	0,02	2	500
3	0,10	1	300
4	0,10	2	500

La compañía de seguros quiere cobrar de este grupo de 1800 personas una cantidad igual al percentil 95 de la distribución de los pagos totales de seguros para este grupo. Además, quiere que la parte de esa cantidad de cada persona sea proporcional al pago esperado del seguro de la persona.

La parte de la persona con el número , cuyo pago promedio es igual a , debe ser . Del requisito del percentil 95 se deduce que . El exceso de valor, , es la prima de riesgo, y se denomina prima de riesgo relativa. Calculemos.

Solución. El valor está determinado por la relación = 0,95, donde S = X 1 + X 2 + ... + X 1800 . Esta declaración de probabilidad es equivalente a lo siguiente:

De acuerdo con lo dicho sobre el teorema del límite central en la Sec. 4, aproximamos la distribución de la v.r. distribución normal estándar y usamos su percentil 95, de donde obtenemos:

Para las cuatro clases en que se dividen los asegurados se obtienen los siguientes resultados:

k	q k	b k	Promedio b k q k	Varianza b 2 k q k (1-q k)	nk
1	0,02	1	0,02	0,0196	500
2	0,02	2	0,04	0,0784	500
3	0,10	1	0,10	0,0900	300
4	0,10	2	0,20	0,3600	500

De este modo,

Por lo tanto, la prima de riesgo relativa es

Ejemplo 5.2. Los clientes de una compañía de seguros de automóviles se dividen en dos clases:

Clase	Número en clase	Probabilidad de ocurrencia evento asegurado	Distribución de pagos de seguros, parámetros exponenciales truncados distribución
k				L
1	500	0,10	1	2,5
2	2000	0,05	2	5,0

La distribución exponencial truncada está definida por la función de distribución

Esta es una distribución de tipo mixto con una función de densidad. , y un "grupo" de masa probabilística en un punto L. El gráfico de esta función de distribución se muestra en la Figura 5.1.

Arroz. 5.1. Distribución exponencial truncada

Como antes, la probabilidad de que el monto total de los pagos del seguro exceda el monto recaudado de los asegurados debe ser igual a 0.05. Supondremos que la prima de riesgo relativa debe ser la misma en cada una de las dos clases consideradas. Calculemos.

Solución. Este ejemplo es muy similar al anterior. La única diferencia es que los valores de los pagos de seguros ahora son variables aleatorias.

Primero, obtendremos expresiones para los momentos de la distribución exponencial truncada. Este será un paso preparatorio para aplicar las fórmulas (2.25) y (2.26):

Usando los valores de los parámetros dados en la condición y aplicando las fórmulas (2.25) y (2.26), obtenemos los siguientes resultados:

k	q k	µk	σ 2k	Promedio q k μ k	Dispersión μ 2 k q k (1-q k)+σ 2 k q k	nk
1	0,10	0,9139	0,5828	0,09179	0,13411	500
2	0,05	0,5000	0,2498	0,02500	0,02436	2000

Asi que, S, el monto total de los pagos del seguro, tiene momentos

La condición para la definición sigue siendo la misma que en el ejemplo 5.1, a saber,

Usando nuevamente la aproximación de distribución normal, obtenemos

Ejemplo 5.3. La cartera de la aseguradora incluye 16.000 contratos de seguros de deceso por un período de un año según el siguiente cuadro:

La probabilidad de un evento asegurado q para cada uno de los 16.000 clientes (se supone que estos eventos son independientes entre sí) es 0,02. La empresa quiere establecer su propia tasa de retención. Para cada asegurado, el nivel de retención propia es el valor por debajo del cual esta empresa (empresa cedente) realiza pagos de forma independiente, y los pagos que superan este valor son cubiertos bajo el contrato de reaseguro por otra empresa (reaseguradora).

Por ejemplo, si la tasa de retención propia es de 200.000, entonces la compañía reserva una cobertura de hasta 20.000 para cada asegurado y compra reaseguro para cubrir la diferencia entre la prima y la cantidad de 20.000 para cada uno de los 4.500 asegurados cuyas primas de seguro superan los 20.000.

La compañía elige como criterio de decisión la minimización de la probabilidad de que los siniestros de seguros dejados en su propia deducción, más el monto pagado por el reaseguro, superen la cantidad de 8.250.000 Costos del reaseguro 0,025 por unidad de cobertura (es decir, 125% de lo esperado el valor de los pagos del seguro por unidad 0,02).

Consideramos que la cartera en cuestión está cerrada: los nuevos contratos de seguros suscritos durante el año en curso no serán tenidos en cuenta en el proceso de toma de decisiones descrito.

Solución parcial. Primero hagamos todos los cálculos, eligiendo como unidad de pago 10 000. Como ilustración, supongamos que c. en. S es el monto de los pagos que quedan por deducción propia, tiene la siguiente forma:

A estos pagos de seguros dejados en su propia deducción S, se suma el importe de las primas de reaseguro. En total, el monto total de la cobertura según este esquema es

La cantidad que queda en la deducción propia es igual a

Por lo tanto, el valor total reasegurado es 35 000-24 000 = 11 000 y el costo del reaseguro es

Por lo tanto, en el nivel de retención propia igual a 2, los pagos de seguro que quedan en la retención propia más el costo del reaseguro son . El criterio de decisión se basa en la probabilidad de que este total supere los 825,

Utilizando la distribución normal, obtenemos que este valor es aproximadamente igual a 0,0062.

Los valores medios de los pagos de seguros por exceso de pérdida, como uno de los tipos de reaseguro, se pueden aproximar utilizando la distribución normal como distribución de los pagos totales de seguros.

Deje que los pagos totales de seguros X tengan una distribución normal con media y varianza

Ejemplo 5.4. Consideremos una cartera de seguros, como en un ejemplo 5.3. Encontremos la expectativa matemática de la cantidad de pagos de seguro bajo el contrato de seguro por el exceso de falta de rentabilidad, si

(a) no existe reaseguro individual y el deducible incondicional se fija en 7.500.000

(b) Se establece una retención personal de 20.000 en los contratos de seguros individuales y la franquicia incondicional para la cartera es de 5.300.000.

Solución.

(a) En ausencia de reaseguro individual y en la transición a 10.000 como moneda

aplicando la fórmula (5.2) se obtiene

que es la suma de 43.770 en las unidades originales.

(b) En la Figura 5.3, obtenemos que la media y la varianza de las primas totales para un deducible individual de 20 000 son 480 y 784, respectivamente, usando 10 000 como unidad. Por lo tanto, =28.

aplicando la fórmula (5.2) se obtiene

que es la suma de 4140 en las unidades originales.